 im
Studiengang Mechatronik
im
Studiengang Mechatronik
S T U D I E N A R B E I T WS 2002 / 03
 im
Studiengang Mechatronik
im
Studiengang Mechatronik
Entwicklung einer elektrischen Schaltung
zur
Auswertung kleiner Kapazitätsänderungen
Bearbeitet
von:
Aleksandar
Andjic,
Andreas
Tschürtz
Betreut
durch:
Prof.
Dipl.-Phys. Dipl.-Ing. Edmund Schiessle
1.
Einführung in die Problematik der Messung einer Kapazitätsänderung im femto Farad Bereich.
2.
Die
„zweifache Frequenzmessung“ und deren Schaltungsaufbau
2.1
Der
Oszillator
2.2
Kalibrierung
2.3 Messung der Kapazitätsänderung
2.3.1
Messprotokolle,
Messung Cx, Messreihe
1, ohne Schirmung
2.3.2
Maximaler Fehler
2.3.3
Messprotokolle, Messung Cx
2.3.4
Simulation einer Kapazitätsänderung
3.
Möglichkeiten
der Schaltungserweiterung
3.1
Messen von
Induktivitätsänderungen
3.2
Frequenzmessung -,
und Auswertung mit einem Mikrocontroller mit Kalibrierung
4.
Zusammenfassung,
Auswertung und Fazit
1.
Einführung in die Problematik der Messung einer Kapazitätsänderung
im femto Farad Bereich
(1
femto Farad = 0.001 piko Farad).
Viele elektrische Schaltungen zur Messung von Kapazitäten sind aufgrund Ihres Schaltungsaufbaus nicht in der Lage, Kapazitätsänderungen im femto Farad Bereich zu messen bzw. genau anzuzeigen. Das Problem resultiert aus der Methode der jeweiligen Kapazitätsmessung.
Unsere Aufgabenstellung bei
dieser Studienarbeit war es, eine Schaltung zu entwickeln, die es ermöglicht,
diese geringsten Kapazitätsänderungen zu messen und auszuwerten.
2.
Die „Zweifache Frequenzmessung“ und deren
Schaltungsaufbau
Die Messung der Kapazitätsänderung erfolgt bei unserer Schaltung (siehe Bild 2a) über den vergleich von Frequenzen. Der Operationsverstärker IC1 welcher den wesentlichen Teil der Schaltung darstellt, bringt den Schwingkreis bestehend aus L1 und C1 auf dessen Resonanzfrequenz f1. Die normale Leerlauffrequenz der Schaltung liegt bei einer Frequenz von ca. 740kHz. Zur Messung werden nun Messobjekte so an die Schaltung angeschlossen, dass die Resonanzfrequenz f2, des nun geänderten Schwingkreises, unterhalb der Leerlauffrequenz f1 liegt. Das heißt, Kondensatoren werden parallel zur Schwingkreiskapazität C1 geschaltet. Zusammen mit der Leerlauffrequenz f1 und der Resonanzfrequenz f2 kann nun der Wert des Messobjektes berechnet werden.
Um nun bei L1 und C1 Bauteile hoher Toleranz (10%) verwenden zu können, werden diese vor der Messung, während einer Kalibrierungs-Phase, mit einem genauen „Referenz“ -Kondensator C2 (ca. 0,5%) ausgemessen. C2 ist also das einzige genaue Bauteil in der Schaltung.
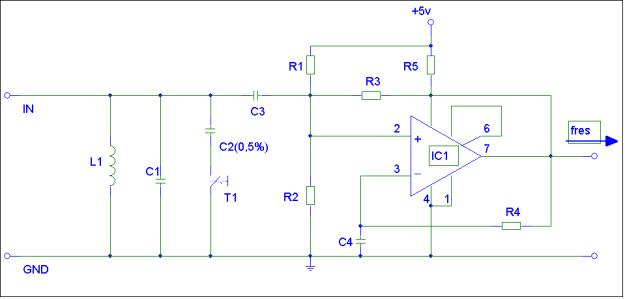
Bild 2a
2.1 Der Oszillator
Das
Herz des L/C-Meters ist der Oszillator. Die Funktionsweise des Oszillators lässt
sich am besten verstehen, wenn man sich vorstellt, dass das Ausgangssignal des
Operationsverstärkers LM311 (IC1)
eine Rechteckschwingung auf der Resonanzfrequenz des aus L1 und C1
bestehenden Kreises ist. Diese Spannung wird dem Schwingkreis über R3
und C3 zugeführt. Der
Schwingkreis filtert die sinusförmige Grundschwingung heraus, welche dann an
den Eingang des Komparators angelegt wird und als Rechteckschwingung wieder an
seinem Ausgang erscheint. Auf diese Weise entsteht ein kontinuierliches
Rechtecksignal.
Wenn nach dem Einschalten die Eingangsspannung an Pin 2 des LM311 größer wird als die Hälfte der Betriebsspannung, die durch den Spannungsteiler, bestehend aus R1 und R2, erzeugt wird, führt der Ausgang an Pin 7 High - Pegel in die Höhe der Betriebsspannung. Dieser High - Pegel lädt C4 über R4 solange auf, bis die Spannung an Pin 3 genauso groß ist wie die Spannung an Pin 2. Dann schaltet der Ausgang wieder auf Low - Pegel, was eine Spannungsspitze im Schwingkreis erzeugt, so dass er auf seiner Resonanzfrequenz nachschwingt. Diese Spannung wird in eine Rechteckschwingung auf der Resonanzfrequenz des Schwingkreises umgeformt, was die Schwingung aufrechterhält.
Während der Kalibrierung wird die Leerlauffrequenz f1 gemessen, welche bei offenen Klemmen durch L1 und C1 bestimmt wird.
Damit erhält man ein Frequenz
von:
![]() Gleichung
2-1
Gleichung
2-1
Diese Gleichung enthält zwei
Unbekannte und lässt sich nicht nach L1
oder C1 auflösen. Um noch
eine zweite Gleichung zu erhalten wird ein Kondensator (C2) mit bekanntem Wert in die Schaltung eingefügt. Dazu
wird der Taster T1 gedrückt so dass
der Kondensator C2 (einen
1nF Kondensator mit 0,5% Genauigkeit) in die Schaltung (Bild 2b) eingefügt
wird. Damit lässt sich die Frequenz neu bestimmen:
![]() Gleichung
2-2
Gleichung
2-2
Diese
beiden Gleichungen können nach C1
und L1 aufgelöst werden:
![]() Gleichung
2-3
Gleichung
2-3
![]() Gleichung
2-4
Gleichung
2-4
Da die exakten Werte von L1 und C1 ausgemessen werden, können Bauelemente mit Toleranzen von bis zu 10% eingesetzt werden. Die Genauigkeit des Messgerätes hängt allein von C2 ab, der eine Toleranz von 0,5% hat. Die Schaltung sollte bei der Messung von kleinen Kapazitäten des öfteren neu kalibriert werden, um eine größt mögliche Genauigkeit zu erreichen. Zusätzlich sollte auf eine gewisse Aufwärmzeit der Schaltung geachtet werden, damit sich deren Bauteile, und somit deren Schwingkreis, thermisch stabilisieren.
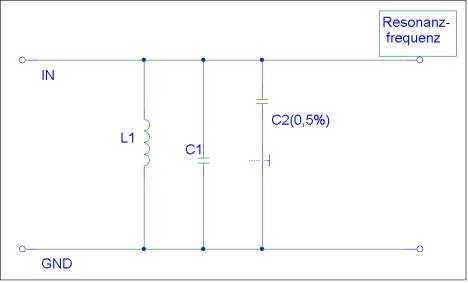
Bild 2b
2.3
Messung
der Kapazitätsänderungen
Nun wird der Kondensator Cx, dessen Kapazitätsänderung wir messen wollen,
parallel (siehe Bild 2c) zu L1
und C1 gelegt (Taster T1
ist nicht gedrückt). Die nun sich einstellende
Frequenz fx spiegelt die
Kapazität des Kondensators Cx
und gleichzeitig dessen Änderung wieder. Die Gesamtkapazität folgt somit aus
der Summe C1
+ Cx. Aus Gl.
2-5 für fx, sowie aus Gl.
2-1 bilden wir die Gl.
2-6, die den Wert für Cx
liefert.
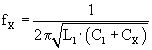 Gleichung
2- 5
Gleichung
2- 5
![]() Gleichung
2-1
Gleichung
2-1
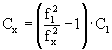 Gleichung
2- 6
Gleichung
2- 6
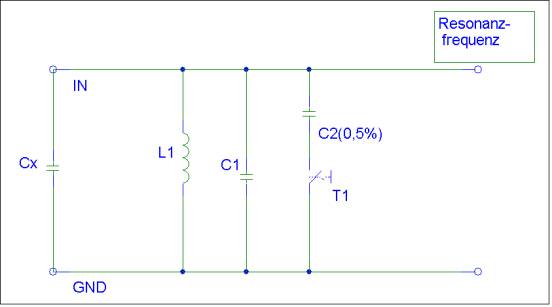
Bild 2c
2.3.1 Messung kleinster Kapazitätsänderungen
Messprotokolle (Messreihe 1, ohne Schirmung)
Messung der Frequenzen mit Philips Frequenzzähler
| Leerlauffrequenz | Kalibrierfrequenz | ||
| f1 (Hz) | f2 (Hz) | ||
| 715909 | Durchschnitt für f1: | 465588 | Durchschnitt für f2: |
| 715903 | 715.880 Hz | 465587 | 465.590 Hz |
| 715898 | 465589 | ||
| 715893 | f1 max.: | 465589 | f2 max.: |
| 715885 | 715.909 Hz | 465591 | 465.596 Hz |
| 715881 | 465590 | ||
| 715882 | f1 min: | 465590 | f2 min: |
| 715884 | 715.881 Hz | 465591 | 465.587 Hz |
| 715883 | 465592 | ||
| 715884 | f1 min/max Differenz: | 465591 | f2 min/max Differenz: |
| 715881 | 28 Hz | 465592 | 9 Hz |
| 715874 | 465594 | ||
| 715870 | 465596 | ||
| 715865 | 465594 | ||
| 715875 | 465592 | ||
| 715882 | 465591 | ||
| 715885 | 465596 | ||
| 715891 | 465588 | ||
| 715895 | 465590 |
Berechnung von C1min, C1max mit C2=1000pF ±1% :
C1min (mit f1max und f2min) = 732,943 pF
C1max (mit f1min und f2max) = 733,092 pF
Da hier nicht die "absolut Genauigkeit" (Kapazitiver Gesamtwert) sondern später die Genauigkeit der Kapazitätsänderung von Interesse ist, rechnen wir nur die "Frequenzungenauigkeit" mit ein, und nicht die Ungenauigkeit des Referenzkondensators C2 mit ±1%.
2.3.2 Maximaler Fehler bei der Bestimmung des Cx
Hier ergibt sich durch die "ungenaue" Frequenzmessung folgendes Problem:
Setzt man die Gl. für C1 in die Gl. für Cx ein so kann man den maximalen Fehler berechnen, welcher für Cx erfolgen würde.
- fx nehmen wir mit 600.000 Hz an,
Hieraus berechnet: Cx min ( f1min und f2 min) = 310.496 pF
und Cx max ( f1max und f2max) = 310,555 pF
Cx min/max Differenz: 0,059 pF = 59 fF
Man muss bei diesem Messergebnis beachten, dass hier rein nur die Frequenzdifferenzen berücksichtigt wurden, welche vom Frequenzzähler angezeigt wurden. Die zusätzliche Abweichung die durch den Fehler des Frequenzzählers entstehen, wurden nicht berücksichtigt (idealer Frequenzzähler). Somit entsteht die Cx min/max Differenz durch äußere Fremdkapazitäten und andere Einflüsse, welche eine ausreichende Stabilität des Schwingkreises nicht zulassen.
2.3.3 Messung kleinster Kapazitätsänderungen
Messprotokolle (Messreihe 2, mit Schirmung)
| Messung 1 | Messung 2 | |||||
| Leerlauffreq. | Kalibrierfreq. | Leerlauffreq. | Kalibrierfreq. | |||
| f1 (Hz) | f2(Hz) | f1(Hz) | f2(Hz) | |||
| 696817 | 460712 | 696767 | 460687 | |||
| 696816 | 460713 | 696768 | 460687 | |||
| 696817 | Durchschnitt | 460713 | 696768 | Durchschnitt | 460688 | |
| 696817 | für f1 | 460714 | 696768 | für f1 | 460687 | |
| 696816 | 696816 Hz | 460713 | 696767 | 696766 Hz | 460688 | |
| 696817 | 460714 | 696767 | 460688 | |||
| 696817 | 460713 | 696768 | 460688 | |||
| 696816 | 460714 | 696768 | 460688 | |||
| 696816 | Durchschnitt | 460714 | 696767 | Durchschnitt | 460687 | |
| 696816 | für f2 | 460714 | 696768 | für f2 | 460688 | |
| 696816 | 460714 Hz | 460714 | 696768 | 460688 Hz | 460689 | |
| 696816 | 460714 | 696767 | 460688 | |||
| 696816 | 460714 | 696767 | 460688 | |||
| 696816 | Ber. C1 mit Gl 2-3 | 460715 | 696767 | Ber. C1 mit Gl 2-3 | 460687 | |
| 696816 | 776,660 pF | 460715 | 696766 | 776,670 pF | 460688 | |
| 696816 | 460715 | 696766 | 460689 | |||
| 696815 | 460715 | 696767 | 460688 | |||
| 696815 | 460716 | 696765 | 460688 | |||
| 696816 | 460715 | 696766 | 460688 | |||
| 696816 | 460716 | 696765 | 460688 | |||
| 698816 | 460716 | 696764 | 460687 | |||
| Messung 3 | Messung 4 | |||||
| Leerlauffreq. | Kalibrierfreq. | Leerlauffreq. | Kalibrierfreq. | |||
| f1(Hz) | f2(Hz) | f1(Hz) | f2(Hz) | |||
| 696842 | 460726 | 696809 | 460729 | |||
| 696843 | 460727 | 696810 | 460729 | |||
| 696842 | Durchschnitt | 460727 | 696810 | Durchschnitt | 460729 | |
| 696842 | für f1 | 460727 | 696809 | für f1 | 460729 | |
| 696842 | 696842 Hz | 460728 | 696809 | 696810 Hz | 460728 | |
| 696841 | 460728 | 696809 | 460728 | |||
| 696842 | 460727 | 696810 | 460728 | |||
| 696841 | 460727 | 696810 | 460728 | |||
| 696842 | Durchschnitt | 460727 | 696810 | Durchschnitt | 460729 | |
| 696842 | für f2 | 460728 | 696810 | für f2 | 460728 | |
| 696842 | 460728 Hz | 460727 | 696811 | 460728 Hz | 460728 | |
| 696842 | 460728 | 696811 | 460728 | |||
| 696842 | 460728 | 696810 | 460728 | |||
| 696841 | Ber. C1 mit Gl 2-3 | 460728 | 696811 | Ber. C1 mit Gl 2-3 | 460728 | |
| 696842 | 776,641 pF | 460728 | 696812 | 776,768 pF | 460728 | |
| 696842 | 460728 | 696812 | 460729 | |||
| 696842 | 460729 | 696812 | 460728 | |||
| 696842 | 460728 | 696813 | 460728 | |||
| 696841 | 460728 | 696813 | 460728 | |||
| 696842 | 460728 | 696814 | 460728 | |||
| 696842 | 460728 | 696813 | 460729 |
Erläuterung zu den
Messergebnissen zu 2.3.3
Aus den Messergebnissen ist zu sehen, dass Aufgrund der Schirmung der Schaltung sich die Stabilität der Frequenzen wesentlich verbessert. Jedoch ist ebenfalls zu sehen, dass sich eine art „Drift“ der Frequenzen nach längeren Zeitintervallen (zeitlicher Abstand zwischen den Messreihen) einstellt. Dieses Problem könnte jedoch mit der „ständigen Kalibrierung“ mit einem Mikrocontroller (Abschn. 3.2) behoben werden.
2.3.4 Simulation einer Kapazitätsänderung im fF
-
Bereich
Der Versuchsaufbau:
Im Bild zu sehen der digitale Messschieber auf welchem
wir 2 „Kondensatorplatten“ angebracht haben. Mit den nun bekannten
Plattengrößen,
Kapazitätsberechnung:
Plattendurchmesser: d=7,5mm => A=4,4179mm2
Simulierte
Kapazitäten: 1.) 0,1pF =
100fF
2.) 0,15pF = 150fF
=> für Abstand l der Platten mit l=Eo . A /C la=3,91mm , lb=2,61mm (Pos.
1, Pos. 2)
|
Messung
1 |
|
|
Änderung
der Position |
|
zu
Messung 1: |
|
||
|
fx
Pos 1 |
fx
Pos 2 |
|
Pos
i |
fx |
|
fx Pos1 = 694915, fx Pos2 = 694913 |
||
|
694914 |
694911 |
|
Pos
1 |
694963 |
|
daraus
folgt für Cx mit C1= 776,660 pF |
||
|
694915 |
694912 |
|
Pos
2 |
694942 |
|
und f1= 696816 Hz |
||
|
694915 |
694913 |
|
Pos
1 |
694968 |
|
Cx Pos1 = 4,255pF
Cx Pos2 = 4,260pF |
||
|
694916 |
694913 |
|
Pos
2 |
694940 |
|
|
|
|
|
694915 |
694913 |
|
Pos
1 |
694971 |
|
|
|
|
|
|
|
|
Pos
2 |
694943 |
|
zu
Messung 2: |
|
|
|
Messung
2 |
|
|
Pos
1 |
694974 |
|
fx Pos1= 694957, fx Pos2 = 694932 |
||
|
fx
Pos 1 |
fx
Pos 2 |
|
Pos
2 |
694949 |
|
daraus
folgt für Cx mit C1= 776,660 pF |
||
|
694957 |
694931 |
|
Pos
1 |
694977 |
|
und f1= 696816Hz |
||
|
694957 |
694932 |
|
Pos
2 |
694941 |
|
Cx Pos1 = 4,161pF Cx
Pos2 = 4,217pF |
||
|
694956 |
694931 |
|
Pos
1 |
694974 |
|
|
|
|
|
694957 |
694931 |
|
Pos
2 |
694949 |
|
Stellungnahme
zu den Messergebnissen |
||
|
694957 |
694933 |
|
|
|
|
siehe
Abschnitt 4. |
|
|
3. Möglichkeiten der Schaltungserweiterung
3.1
Messen von Induktivitätsänderungen
Mit
ein paar kleinen Änderungen können wir unsere Schaltung zum Messen von
Induktivitätsänderungen benützen (siehe Bild 3a).
Die Schaltung wird hierbei um den Schalter Cx
Sw
und Lx
Sw erweitert, um eine
„Umschaltung“ zwischen den jeweiligen Messarten
zu ermöglichen.
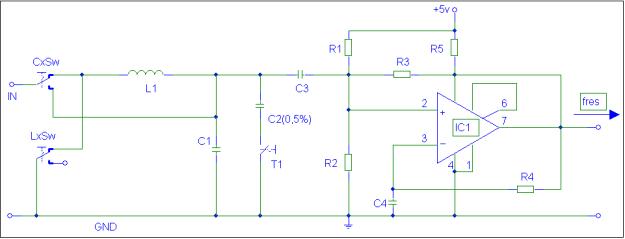
Bild
3a
Sind
Schalter Lx Sw und Cx Sw unbetätigt
so messen wir die Frequenz f1 .
Wird der Schalter Lx
Sw gedrückt,
wird die unbekannte Spule Lx (siehe Bild 3b) in Reihe zu L1 geschaltet. Die Gesamtinduktivität ist dann die Summe
aus L1
+
Lx.
Damit ändert sich die Frequenz nach Gleichung
3-1 wie folgt:
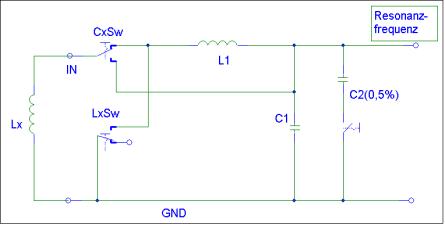
![]()
Gleichung 3-1
Bild 3b
Diese Gleichung kann gelöst
werden, indem man zusätzlich die Gl. 2-1 für f1 verwendet. Damit erhält man:
![]() Gleichung
2-1
Gleichung
2-1
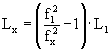 Gleichung 3-2
Gleichung 3-2
3.2 Frequenzmessung
-,
und Auswertung mit einem Mikrocontroller,
sowie dessen Vorteile durch die Möglichkeit der permanenten Kalibrierung
Der Mikrocontroller hat hier
die Aufgabe die Frequenzen vom Analogteil zu messen und Auszuwerten (siehe Bild
3c).
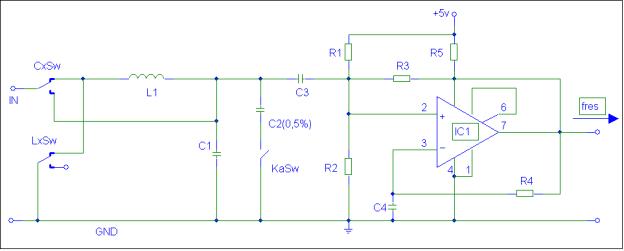
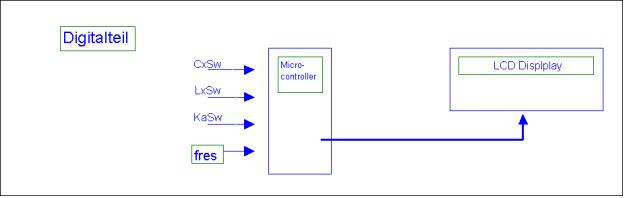
Bild 3c
Die
Vorteile des Mikrocontrollers:
Der
Mikrocontroller ermöglicht uns eine ständige Neukalibrierung der Schaltung,
und deren Referenzfrequenz. D.h. durch das Kalibrieren werden die Fehler, welche
durch äußere Einflüsse, sowie durch den „thermischem Nullpunktdrift“
hervorgerufen werden minimiert. Zudem erleichtert er die Auswertung, indem man
ihn so programmiert, dass er die Berechnung des Cx
bzw. des Lx vollkommen
selbständig übernimmt, und diese Ergebnisse einem Display übermittelt.
4.
Zusammenfassung, Auswertung und Fazit
Aus
den vorangegangen Versuchen und Messreihen ist ersichtlich, dass die von uns
gebaute Schaltung es ermöglicht kleinste Kapazitätsänderungen zu messen,
jedoch nicht in dem von uns angestrebten femto - Farad Bereich.
Zur Auswertung der
Frequenzen sollte unbedingt, wie in Kapitel 3.2 beschrieben, ein Mikrocontroller
verwendet werden, um die Fehler durch Temperaturänderungen, und Nullpunktdrift
durch die „permanente Kalibrierung“ weitgehend zu kompensieren.
Aus den Messergebnissen der Simulation der Kapazitätsänderung mit dem
digitalen Messschieber (Kapitel 2.4.4) ist die zu große Einwirkung von äußeren
Störspannungen, -Kapazitäten gut ersichtlich. Bei der Simulation einer Kapazitätsänderung
von 50 femto - Farad sahen wir somit die Grenzen unseres Schaltungs-, und
Versuchsaufbaus.
Weiterhin ist anzumerken dass der in unserem Schwingkreis benützte Keramikkondensator C1 nicht als ideales Bauteil zu sehen ist. Durch mehrere Versuche stellten wir fest dass es zu unerwünschten Frequenzschwankungen beim auf-, und abschalten des Referenzkondensator C2 kam. Für eine stabilere Frequenz wäre ein Styroflexkondensator somit wahrscheinlich besser geeignet.
Abschließend ist zu bemerken, dass wir durch den engen Zeitraum den wir zur
Verfügung hatten, unser Versuchs- und Testpart sehr gering ausgefallen ist.
Durch den Einsatz einer speziell erstellten Platine sowie einer dafür
optimierten Schirmung könnte man sicher mehr aus der Schaltung gewinnen. Der so
oft angesprochene Einbau eines Mikrocontrollers würde zum vereinfachen der
Messungen wesentlich beitragen.
Auf diesem Wege möchten wir uns noch bei allen Mitwirkenden recht herzlich
bedanken, zum einen bei Herrn Strobel für die Bereitstellung des
Elektroniklabors, und zum anderen ganz besonders bei Herrn Prof. Dipl.-Phys.
Dipl.-Ing. Schiessle, ohne den dieses Projekt nicht realisiert worden wäre.